Sistema de ecuaciones lineales
En matemáticas y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto deecuaciones lineales sobre un cuerpo o un anillo conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:
El problema consiste en encontrar los valores desconocidos de las variables x1, x2 y x3 que satisfacen las tres ecuaciones.
El problema de los sistemas lineales de ecuaciones es uno de los más antiguos de la matemática y tiene una infinidad de aplicaciones, como en procesamiento digital de señales,análisis estructural, estimación, predicción y más generalmente en programación lineal así como en la aproximación de problemas no lineales de análisis numérico.
Clasificación de sistemas
En realidad, los sistemas de ecuaciones se pueden clasificar por diversos motivos, es decir, atendiendo a diversas propiedades de los mismos. Por ejemplo, se pueden clasificar según el grado de las ecuaciones. Tendríamos entonces:
- Sistema lineal: si todas las ecuaciones son lineales.
- Sistema no lineal: si no todas las ecuaciones son lineales.
De estos dos tipos de sistemas, nosotros estamos tratando en esta Unidad los sistemas lineales.
Por otro lado, también se pueden clasificar los sistemas según el número de ecuaciones o de incógnitas que tengan, es decir, podríamos hablar entonces de:
- Sistemas de dos ecuaciones.
- Sistemas de tres ecuaciones.
- etc. . . . .
O bien de:
- Sistemas de una incógnita.
- Sistemas de dos incógnitas.
- Sistemas de tres incógnitas.
- etc. . . . .
Parámetros e interpretación geométrica de un sistema
Eliminación de Gauss-Jordan
En matemáticas, la eliminación Gaussiana, eliminación de Gauss o eliminación de Gauss-Jordan,
lineal para determinar las soluciones de un sistema de ecuaciones lineales, encontrar matrices e inversas.
Un sistema de ecuaciones se resuelve por el método de Gauss cuando se obtienen sus soluciones mediante
la reducción del sistema dado a otro equivalente en el que cada ecuación tiene una incógnita menos que
la anterior. Cuando se aplica este proceso, la matriz resultante se conoce como: "forma escalonada".
Algoritmo de eliminación de Gauss-Jordan
- Ir a la columna no cero extrema izquierda
- Si el primer renglón tiene un cero en esta columna, intercambiarlo con otro que no lo tenga
- Luego, obtener ceros debajo de este elemento delantero, sumando múltiplos adecuados del renglón
- superior a los renglones debajo de él
- Cubrir el renglón superior y repetir el proceso anterior con la submatriz restante. Repetir con el resto de
- los renglones (en este punto la matriz se encuentra en la forma de escalón)
- Comenzando con el último renglón no cero, avanzar hacia arriba: para cada renglón obtener un 1 delantero
- e introducir ceros arriba de este sumando múltiplos correspondientes a los renglones correspondientes
Una variante interesante de la eliminación de Gauss es la que llamamos eliminación de Gauss-Jordan,
(debido al mencionado Gauss y a Wilhelm Jordan), esta consiste en ir obteniendo los 1 delanteros durante los
pasos uno al cuatro (llamados paso directo) así para cuando estos finalicen ya se obtendrá la matriz en forma
escalonada reducida
[editar]Ejemplo
Supongamos que es necesario encontrar los números x, y, z, que satisfacen simultáneamente estas ecuaciones:
Esto es llamado un sistema lineal de ecuaciones. El objetivo es reducir el sistema a otro equivalente, que tenga
las mismas soluciones. Las operaciones (llamadas elementales) son estas:
- Multiplicar una ecuación por un escalar no nulo.
- Intercambiar de posición dos ecuaciones
- Sumar a una ecuación un múltiplo de otra.
Estas operaciones pueden representarse con matrices elementales que se usan también en otros procedimientos
como la factorización LU o la diagonalización por congruencia de una matriz simétrica.
En nuestro ejemplo, eliminamos x de la segunda ecuación sumando 3/2 veces la primera ecuación a la segunda
y después sumamos la primera ecuación a la tercera. El resultado es:
Ahora eliminamos y de la primera ecuación sumando -2 veces la segunda ecuación a la primera, y sumamos
-4 veces la segunda ecuación a la tercera para eliminar y.
Finalmente eliminamos z de la primera ecuación sumando -2 veces la tercera ecuación a la primera, y sumando
1/2 veces la tercera ecuación a la segunda para eliminar z.
Despejando, podemos ver las soluciones:
Para clarificar los pasos (y es en realidad lo que las computadoras manejan), se trabaja con la matriz aumentada.
Podemos ver los 3 pasos en su notación matricial:
Primero:
Después,
Por último.
Si el sistema fuera incompatible, entonces nos encontraríamos con una fila como esta:
Que representa la ecuación: 0x + 0y + 0z = 1, es decir, 0 = 1 que no tiene solución.
[editar]Forma escalonada y escalonada reducida
Dos formas especiales de matrices son la escalonada y la escalonada reducida. Una matriz puede tener las
siguientes propiedades:
- Todas las filas cero están en la parte inferior de la matriz.
- El elemento delantero de cada fila diferente de cero, éste es llamado "pivote"; éstos están a la derecha del
- elemento delantero de la fila anterior (esto supone que todos los elementos debajo de un pivote son cero).
Si una matriz A cumple con esas propiedades, se dice escalonada. Además, cumpliendo estas otras condiciones,
decimos que la matriz se encuentra en la forma reducida de renglón escalón o tan solo en forma escalonada
reducida.
- Todos los elementos delanteros ("pivotes") son iguales a 1
- Todos los elementos por encima de los pivotes son nulos.
Cuando una matriz representa a un sistema de ecuaciones situaciones como tener una columna de ceros parece
imposible ya que correspondería a una variable que nunca habría aparecido. Sin embargo esta situación puede
presentarse (imaginemos la ecuación de un plano en el espacio en la que no aparece alguna de las componentes,
por ejemplo y+z=0). Así la matriz
también es una matriz escalonada.
Una vez que la matriz del sistema se ha transformado hasta obtener una matriz escalonada reducida es muy fácil
discutirlo (es decir, determinar cuántas soluciones tiene):
- Cuando aparece un pivote en la columna de los términos independientes el sistema es incompatible (no tiene ninguna solución).
- En otro caso el sistema es compatible. Si además el número de pivotes coincide con el número de incógnitas el sistema es compatible determinado (tiene una única solución). Cuando el número de pivotes es menor que el número de incógnitas el sistema es indeterminado (tiene infinitas soluciones que dependen de tantos parámetros como indique la diferencia entre el número de incógnitas y el número de pivotes).
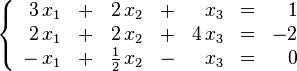



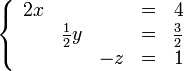






No hay comentarios:
Publicar un comentario
"Cuando las leyes de la matemática se refieren a la realidad, no son ciertas; cuando son ciertas, no se refieren a la realidad."
(Albert Einstein.)
Y la realidad es que debes dejar un comentario ...